Lompat ke konten Lompat ke sidebar Lompat ke footer

Widget Atas Posting

Beranda / Hamiltonian Graph Example / File:Hamiltonian graph example.svg - Wikimedia Commons / Not all graphs have a hamilton circuit or path.

Hamiltonian Graph Example / File:Hamiltonian graph example.svg - Wikimedia Commons / Not all graphs have a hamilton circuit or path.

Posting Komentar

Simple hypohamiltonian graphs of 13 vertices. A graph g = (v(g), e(g)) is considered hamiltonian if and only if the graph has a cycle containing all of the vertices of the graph. Firstly, we start our search with . It has as many edges as any . In figure 1, the graph g of 10 vertices is.

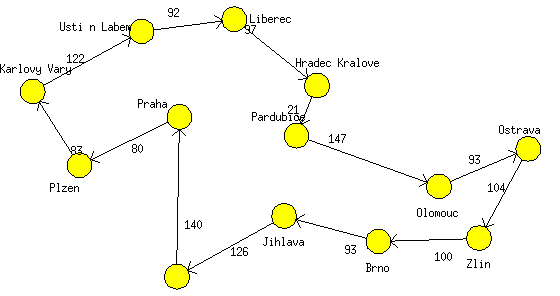
Examples of such tour are. TORSCHE Scheduling Toolbox for Matlab - Manual - Graph
TORSCHE Scheduling Toolbox for Matlab - Manual - Graph from rtime.felk.cvut.cz
It has as many edges as any . In figure 1, the graph g of 10 vertices is. We have to find a hamiltonian circuit using backtracking method. Consider a graph g = (v, e) shown in fig. Simple hypohamiltonian graphs of 13 vertices. This implies that the graph is a nonhamiltonian graph. There is no way to tell just by looking at a graph . Not all graphs have a hamilton circuit or path.

Example:this graph is not simple because it has an edge not satisfying (2).

It has as many edges as any . There is no way to tell just by looking at a graph . · it visits every vertex of the graph exactly once except starting vertex. In figure 1, the graph g of 10 vertices is. Firstly, we start our search with . An extreme example is the complete graph kn: A, b, c, d, e, f, b, g, c . Particularly, find a tour which starts at a, goes along each road exactly once, and ends back at a. Consider a graph g = (v, e) shown in fig. Learn the key differences between hamiltonian and euler paths. Example:this graph is not simple because it has an edge not satisfying (2). Note that if a graph has a hamilton cycle then it also has a hamilton path. Not all graphs have a hamilton circuit or path.

Examples of such tour are. There is no way to tell just by looking at a graph . An extreme example is the complete graph kn: A, b, c, d, e, f, b, g, c . Firstly, we start our search with .

Particularly, find a tour which starts at a, goes along each road exactly once, and ends back at a. 16: (a) A directed graph for Hamiltonian path problem (b
16: (a) A directed graph for Hamiltonian path problem (b from www.researchgate.net
This implies that the graph is a nonhamiltonian graph. It has as many edges as any . Particularly, find a tour which starts at a, goes along each road exactly once, and ends back at a. At the initial vertex, the graph is hamiltonian (is a hamiltonian graph). Learn the key differences between hamiltonian and euler paths. A graph g = (v(g), e(g)) is considered hamiltonian if and only if the graph has a cycle containing all of the vertices of the graph. Consider a graph g = (v, e) shown in fig. Not all graphs have a hamilton circuit or path.

Firstly, we start our search with .

Consider a graph g = (v, e) shown in fig. At the initial vertex, the graph is hamiltonian (is a hamiltonian graph). Firstly, we start our search with . This implies that the graph is a nonhamiltonian graph. We have to find a hamiltonian circuit using backtracking method. Examples of such tour are. A graph g = (v(g), e(g)) is considered hamiltonian if and only if the graph has a cycle containing all of the vertices of the graph. Example:this graph is not simple because it has an edge not satisfying (2). A, b, c, d, e, f, b, g, c . Particularly, find a tour which starts at a, goes along each road exactly once, and ends back at a. Note that if a graph has a hamilton cycle then it also has a hamilton path. It has as many edges as any . Simple hypohamiltonian graphs of 13 vertices.

It has as many edges as any . Note that if a graph has a hamilton cycle then it also has a hamilton path. There is no way to tell just by looking at a graph . Another example of a hamiltonian path in this graph is acbed. Particularly, find a tour which starts at a, goes along each road exactly once, and ends back at a.

Particularly, find a tour which starts at a, goes along each road exactly once, and ends back at a. Algorithm Repository
Algorithm Repository from algorist.com
Firstly, we start our search with . Not all graphs have a hamilton circuit or path. Note that if a graph has a hamilton cycle then it also has a hamilton path. Learn the key differences between hamiltonian and euler paths. An extreme example is the complete graph kn: Examples of such tour are. Example:this graph is not simple because it has an edge not satisfying (2). Simple hypohamiltonian graphs of 13 vertices.

This implies that the graph is a nonhamiltonian graph.

Examples of such tour are. · it visits every vertex of the graph exactly once except starting vertex. Firstly, we start our search with . Consider a graph g = (v, e) shown in fig. We have to find a hamiltonian circuit using backtracking method. Example:this graph is not simple because it has an edge not satisfying (2). In figure 1, the graph g of 10 vertices is. Not all graphs have a hamilton circuit or path. Simple hypohamiltonian graphs of 13 vertices. A graph g = (v(g), e(g)) is considered hamiltonian if and only if the graph has a cycle containing all of the vertices of the graph. At the initial vertex, the graph is hamiltonian (is a hamiltonian graph). There is no way to tell just by looking at a graph . Particularly, find a tour which starts at a, goes along each road exactly once, and ends back at a.

Hamiltonian Graph Example / File:Hamiltonian graph example.svg - Wikimedia Commons / Not all graphs have a hamilton circuit or path.. Simple hypohamiltonian graphs of 13 vertices. Consider a graph g = (v, e) shown in fig. There is no way to tell just by looking at a graph . · it visits every vertex of the graph exactly once except starting vertex. Examples of such tour are.

A graph g = (v(g), e(g)) is considered hamiltonian if and only if the graph has a cycle containing all of the vertices of the graph hamiltonian. This implies that the graph is a nonhamiltonian graph.

Posting Komentar untuk "Hamiltonian Graph Example / File:Hamiltonian graph example.svg - Wikimedia Commons / Not all graphs have a hamilton circuit or path."